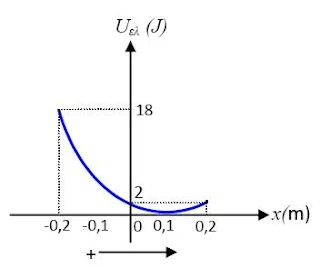
·
Πώς μια πρόσθετη μεταβλητή δύναμη επηρεάζει την α.α.τ.
συστήματος “κατακόρυφο ελατήριο – μάζα”
 Το κάτω άκρο ενός
κατακόρυφου ελατηρίου σταθεράς k1
είναι ακλόνητα στερεωμένο στο δάπεδο ενώ στο πάνω άκρο έχουμε δέσει ένα σώμα
μπάζας m
= 1 kgr
το οποίο εκτελεί α.α.τ. με πλάτος Α = 0,1 m και με συχνότητα f =
5/π Hz. Κάποια στιγμή, συγκεκριμένα όταν
το σώμα διέρχεται από το ανώτερο σημείο της τροχιάς του (αλλιώς, πάνω ακραία
θέση ή Π.Α) αρχίζει να ενεργεί πάνω του, με φορά προς τα πάνω μια επιπλέον κατακόρυφη μεταβλητή δύναμη μέτρου F2 = 300y,
όπου y
η απόσταση του σώματος από το σημείο αυτό.
Το κάτω άκρο ενός
κατακόρυφου ελατηρίου σταθεράς k1
είναι ακλόνητα στερεωμένο στο δάπεδο ενώ στο πάνω άκρο έχουμε δέσει ένα σώμα
μπάζας m
= 1 kgr
το οποίο εκτελεί α.α.τ. με πλάτος Α = 0,1 m και με συχνότητα f =
5/π Hz. Κάποια στιγμή, συγκεκριμένα όταν
το σώμα διέρχεται από το ανώτερο σημείο της τροχιάς του (αλλιώς, πάνω ακραία
θέση ή Π.Α) αρχίζει να ενεργεί πάνω του, με φορά προς τα πάνω μια επιπλέον κατακόρυφη μεταβλητή δύναμη μέτρου F2 = 300y,
όπου y
η απόσταση του σώματος από το σημείο αυτό.
Α.
Να δείξετε ότι το σώμα θα εξακολουθήσει
να κάνει α.α.τ. και να προσδιορίσετε το νέο πλάτος και τη νέα της συχνότητα.
Β.
Πόση είναι η μέγιστη κινητική ενέργεια Κ΄μεγ της νέας ταλάντωσης;
Γ.
Με αρχή μέτρησης του χρόνου (t
= 0) τη στιγμή που αρχίζει να δρα πάνω στο σώμα η δύναμη F2
να εξάγετε τη σχέση που συνδέει την F2
με το χρόνο.
Δίνεται g = 10 m/s2.
Περισσότερα: